В геометрии сумма углов треугольника является фундаментальным свойством, которое имеет важное значение для решения различных задач. Рассмотрим это свойство для выпуклого треугольника.
Содержание
Основная теорема о сумме углов
Для любого выпуклого треугольника сумма величин его внутренних углов постоянна и равна:
| Тип треугольника | Сумма углов |
| Любой выпуклый треугольник | 180° |
Доказательство теоремы
Существует несколько способов доказательства этой теоремы:
- Через параллельные прямые и свойства накрест лежащих углов
- С помощью измерения углов транспортиром
- Путем разрезания треугольника и составления углов
- Используя свойства внешних углов треугольника
Практическое применение
Знание суммы углов треугольника позволяет:
- Находить неизвестные углы в треугольнике
- Доказывать равенство треугольников
- Решать задачи на построение
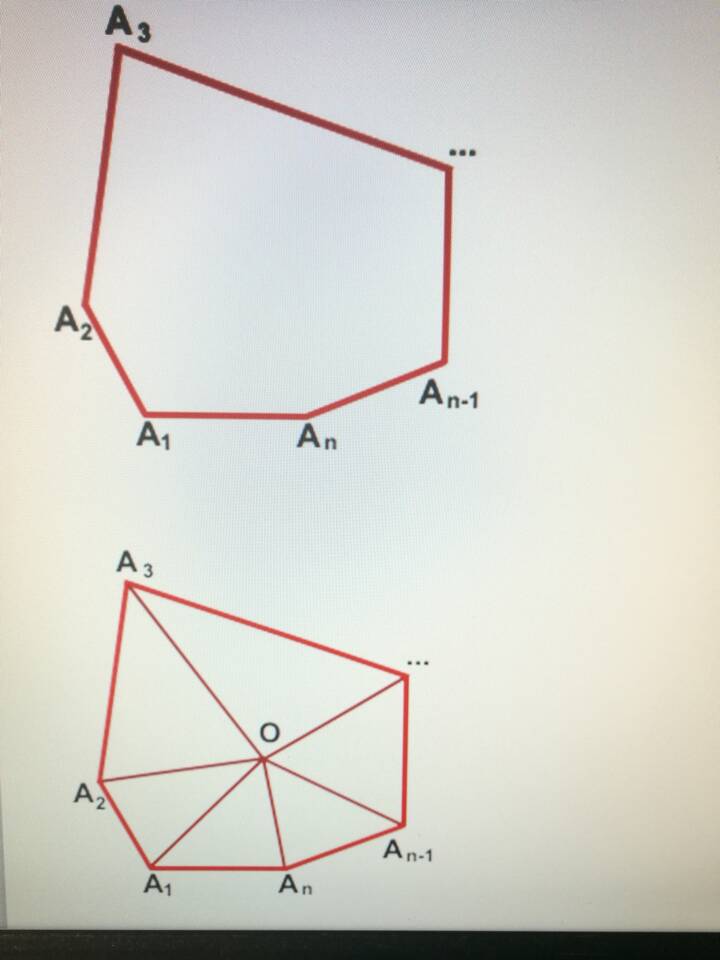
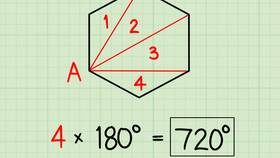
- Анализировать свойства многоугольников
Пример вычисления углов
| Дано | Решение |
| Углы A = 60°, B = 70° | Угол C = 180° - (60° + 70°) = 50° |
| Прямоугольный треугольник с углом 30° | Второй острый угол = 180° - 90° - 30° = 60° |
Особые случаи
Теорема верна для всех видов выпуклых треугольников:
- Остроугольные (все углы < 90°)
- Прямоугольные (один угол = 90°)
- Тупоугольные (один угол > 90°)
- Равносторонние (все углы по 60°)
Таким образом, сумма внутренних углов любого выпуклого треугольника всегда составляет 180 градусов, что является важным свойством евклидовой геометрии.