Сумма внутренних углов шестиугольника - это важная геометрическая характеристика, которая рассчитывается по определенной формуле и имеет практическое значение в различных областях.
Содержание
Сумма внутренних углов шестиугольника - это важная геометрическая характеристика, которая рассчитывается по определенной формуле и имеет практическое значение в различных областях.
Формула расчета суммы углов
Для любого n-угольника сумма внутренних углов вычисляется по формуле:
- S = (n - 2) × 180°
- Где n - количество сторон многоугольника
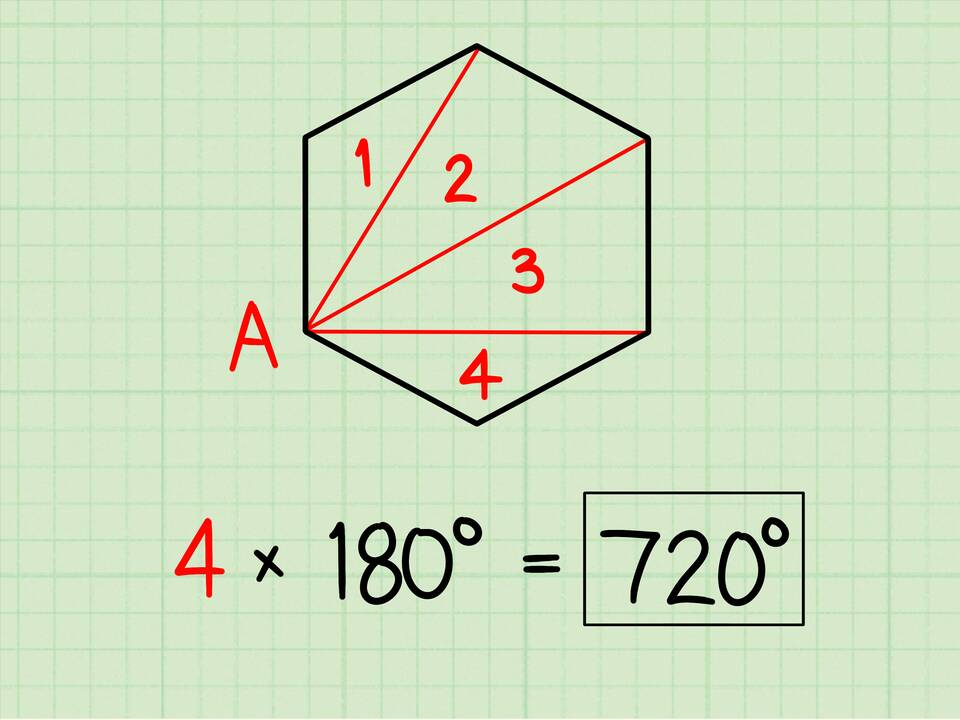
- Для шестиугольника (n = 6): S = (6 - 2) × 180° = 720°
Особенности правильного шестиугольника
| Количество сторон | 6 равных сторон |
| Сумма внутренних углов | 720° |
| Величина одного угла | 120° (в правильном шестиугольнике) |
Практическое применение
- В архитектуре (соты, конструкции зданий)
- В дизайне и декоративном искусстве
- В природных структурах (кристаллические решетки)
- В инженерных расчетах
Сравнение с другими многоугольниками
| Треугольник | 180° |
| Четырехугольник | 360° |
| Пятиугольник | 540° |
| Шестиугольник | 720° |
Доказательство формулы
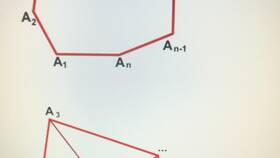
Формула основана на разбиении многоугольника на треугольники:
- Из любой вершины можно провести (n-3) диагонали
- Многоугольник разбивается на (n-2) треугольника
- Сумма углов каждого треугольника 180°
- Общая сумма: (n-2) × 180°
Таким образом, сумма внутренних углов любого шестиугольника всегда равна 720 градусов, а в правильном шестиугольнике каждый угол составляет ровно 120 градусов.
