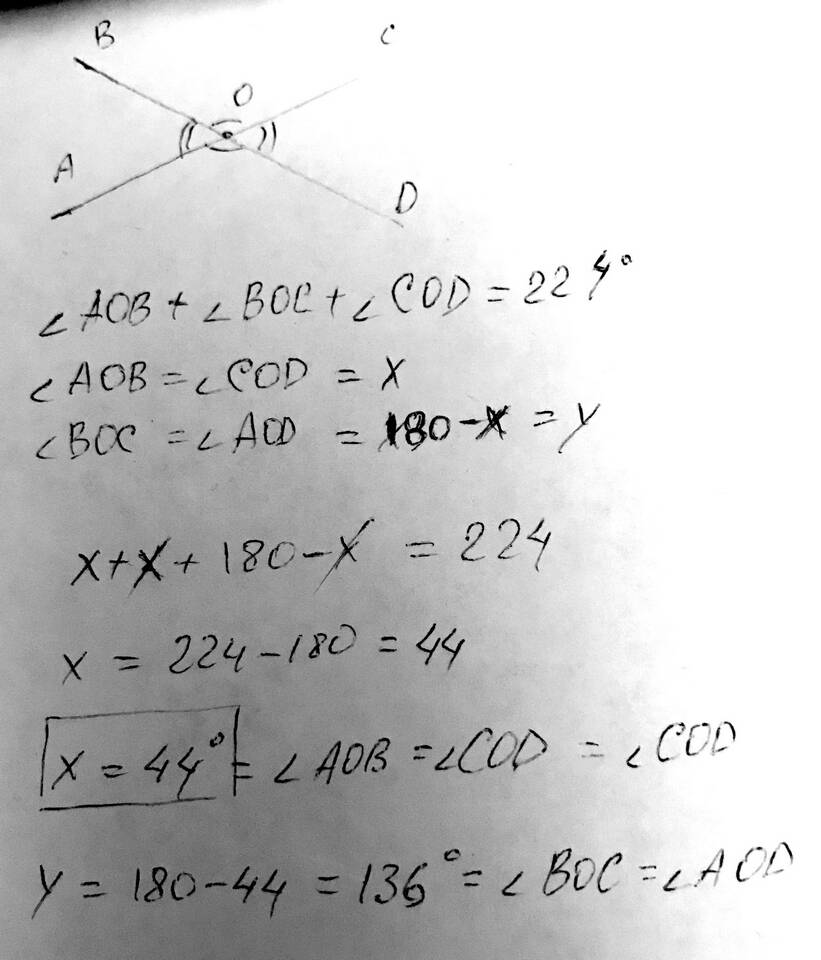Сумма трех углов может иметь разное значение в зависимости от геометрического контекста и типа рассматриваемых углов. Рассмотрим основные случаи и их математические доказательства.
Содержание
Сумма трех углов может иметь разное значение в зависимости от геометрического контекста и типа рассматриваемых углов. Рассмотрим основные случаи и их математические доказательства.
Сумма углов в различных геометрических фигурах
| Фигура | Сумма трех углов |
| Треугольник на плоскости | 180° |
| Треугольник на сфере | Более 180° |
| Три смежных угла | 180° или 360° в зависимости от конфигурации |
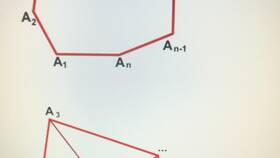
Сумма углов треугольника
Для любого треугольника на евклидовой плоскости сумма трех внутренних углов всегда равна 180°. Это фундаментальное свойство можно доказать:
- Проведем прямую через вершину параллельно противоположной стороне
- Образовавшиеся углы при вершине будут равны углам треугольника
- Сумма углов на прямой составляет 180°
Пример расчета
| Угол A | Угол B | Угол C | Сумма |
| 60° | 60° | 60° | 180° |
| 90° | 45° | 45° | 180° |
Исключения и особые случаи
- В сферической геометрии сумма углов треугольника превышает 180°
- В гиперболической геометрии сумма углов треугольника меньше 180°
- Для трех произвольных углов, не составляющих треугольник, сумма может быть любой
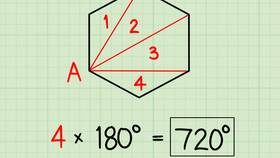
Сумма трех внешних углов треугольника
Сумма трех внешних углов треугольника (по одному при каждой вершине) всегда равна 360°:
- Каждый внешний угол дополняет внутренний до 180°
- Сумма трех внешних: 3×180° - 180° = 360°
Практическое применение
| Область | Использование свойства |
| Архитектура | Расчет углов конструкций |
| Навигация | Определение местоположения |
| Компьютерная графика | Построение трехмерных моделей |
Знание о сумме трех углов треугольника является базовым в геометрии и находит применение во многих научных и практических областях. В зависимости от геометрической системы, эта сумма может изменяться, что важно учитывать при решении задач.
